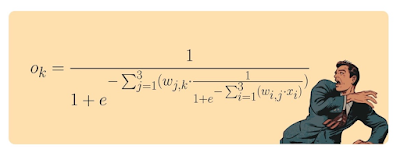
這裡用3 Layer Neural Network為例,每一層都有3個節點,第3層節點的Output的值,可以用下面的公式算出來:
這張圖,出自於「Make Your Own Neural Network」這本書,作者可能想用這道公式,嚇唬大家,至少我被唬到了。我怪這些搞數學的,喜歡把公式寫的又臭又長,拿來唬人有用。但是對於想實作Neural Network的程序員來說,就頭大了。因為要把這種數學公式,翻譯成程式,腦袋要轉好幾個彎。
我常常抱怨,程序員的命不好,除了要翻譯各式各樣的Computer Language,還要看懂數學家寫的數學公式。相對而言,數學家就比較好命了,只要面對數學公式就可以,這一段只是我個人的看法。
國中時,我聽某位數學老師說過,公式,只是為了計算方便。
職場上的我說:Coding Standard,是為了寫程式方便。
最近的我說:遵循Coding Standard的數學公式,是為了方便程式員理解。
今天,我給大家一句話:「數學家,發明公式;程序員,撰寫程式」
這兩種人,各司其職,各有自己的飯碗要顧。
有些數學公式,會以程式的形式出現。喜歡賣弄程式技巧的人,就像這道數學公式一樣,只用一行把程式寫出來。數學公式這樣寫,可能是為了數學家獨特的審美觀,我不是數學家,不便評論。可是,若程序員,複雜的程式一行搞定,那是給接手的人麻煩。
抱怨完了,開始介紹如何實作初步的Neural Network。
一般程序員,大不了就按照這個數學公式,採用裡面的符號,直接寫出程式,這樣很快就交差了事。可是比較有理想的程序員,會想到以後的擴充性,如:3層變成4層。如果程式直接採用裡面的符號,想必將來變成4層,程式就會變得一團糟。避免這種情況發生,就要將Coding Standard的觀念,套用在數學公式上,亦即,拆解並改寫數學公式,使用漂亮可擴充的符號。這件事情,必須由程序員作的,不能期望數學家。程序員在解釋數學公式的同時,也要保留數學公式的原貌,算是對數學家的一種尊重。
還是回歸正題吧。
下圖是3x3 Neural Network,將符號重新命名,以方便將來的實作。有3層,分別是L1, L2, L3。不採用Input Layer, Hidden Layer, Output Layer,而採用編號的方式,是為了方便理解,及將來程式擴充方便。I代表Input的值,O代表Output的值。i, j, k, 就是我們寫程式時,會用到的迴圈變數。用i代表L1的某個節點、j代表L2的某個節點,k代表L3的某個節點。那麼,將來有4層時,要用什麼符號代表L4的節點呢?這個問題先打住。寫程式,先從簡單的開始,等到有一個樣子出現時,再重新定義符號(Refactoring),以方便擴充性。
基本符號定義好了之後,就開始Neural Network是如何運作。我們知道,L1不做任何運算,L2和L3會對權值加總後,做sigmoid運算。
至此,我們用習慣的符號,將Neural Network的程式,寫出來了。接下來,考慮擴充性。寫成Matrix是不錯的方法。對Neural Network有基本觀念的人,知道這些運算,可以用Matrix表示:
這個時候,想買弄數學技巧的程序員,可以寫成下面的式子,這和一開始的數學公式很像,但它是以Matrix形式表達。雖然我覺得,這似乎不是標準的數學公式,但大家應該能看的懂吧。
最後,開始做符號的Refactoring。我們把X, SX, Y這些難以通用的符號換掉,採用I, O, W並且給它們的下標一個編號,代表第幾層。
這樣一來,數學公式,經過這翻更改之後,就算交給資淺的程序員,程式應該很快就可以寫出來吧?而且,也適用於TensorFlow,這個以後再說明。
-Count





沒有留言:
張貼留言