先看2 Layer Neural Network。
我們將training data餵給第2層的目的是調整第1層和第2層的weight。而對於第1層來說，前面沒有weight，就不用做調整weight的事情，就不用BPE (Back-Propagating Errors)。
再來看3 Layer Neural Network。
第1層前面沒有weight，可是在第1層和第2層之前有weight。有weight，就需要調整。問題是，我們的training data是餵給第3層，產生的error，是用來調整第2層和第3層之間的weight。如果我們要調整第1層和第2層的weight，就需要error。
問題是error從那裡來？error可以從第3層傳給第2層。
如何將error合理地分配給第2層的每個節點？依weight比例分配。
下面考慮這種情況。
我習慣先將複雜問題簡化，畫成下圖為3層Neural Network，這是因為探討BPE，至少要3層才有意思。
第1層node及其weight用灰色來表示，因為前面談過，第1層不需要BE，因為前面沒有weight。此圖還標明了e != E，都叫error，意思不同：
E是Error Function，E = Sum ((t - y) ^ 2)，這是將來用Gradient Descent，取最小Error用的。
e是針對單一個Node而言的error，是用來做Back-Propagating Error用的。
為了區分它們的不同，這裡用小寫的e做為Back-Propagating Error，以區別大寫E。區分這兩種Error，非常重要，相信很多人以為e = E，而卡在這一關，
我可以把這張圖畫得更細緻一些。
希望能表達出，第3層node的error，如何按比例分配給第2層的每個node，公式如下。
我們可以把1/(w1+w2)去掉，這樣公式看起來會比較清爽。為何可以這麼做？還記得我們有learning rate嗎？
接下來，在第3層，再多加1個node，看看要如何算出第2層每個node的error。
用Matrix表達這個式子。
還記得以前，第2層 node的input是如何算出來的嗎？
請觀察這兩個式子，發現公式1的weight matrix是公式2的weight matrix的transposing。
讓我們把它改成下面這個樣子，看起來會比較漂亮一些。
這樣寫的好處，除了漂亮之外，程式也會比較好寫。這是因為，程式一開始，為了算出input的值，所建立的weight matrix，可以拿來用在計算第2層的error上，只要將它transposing即可。
現在，我們有了第2層每個node的error值，然後呢？Error的目的是要調整第1層和第2層之間的weight。調整的方法是用Gradient Descent，之前有簡單介紹過：
TensorFlow & Gradient Descent
繼續對TensorFlow的Gradient Descent做逆向工程
是對一個Node做Gradient Descent。現在我們面對的是多個Node，如何做Gradient Descent？待續。
-Count
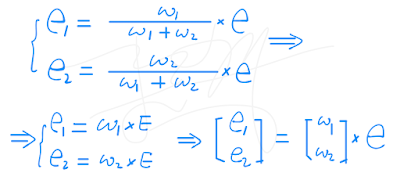
沒有留言:
張貼留言