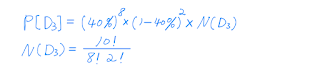在上一篇,
Hoeffding's Inequality,解釋這此不等式的使用方法。本篇用MAC Numbers App及Python幫大家了解這道公式的由來,這對我們日後深入了解Machine Learning,可能會有很大的幫助。

我們假設一種情況是,罐子裡彈珠數量未知,但知道紅色彈珠佔40% (mu),剩下的為綠色。從罐子裡取出一顆彈珠,再放回罐子 (Sampling with Replacement),這樣取放10次裡面,出現紅色彈珠的機率nu與紅色彈珠佔罐子40%,這兩者相差,超出容忍度epsilon 0.3的機率,其上限為多少?
此問題,用圖表示,會比較清楚:
這條線從0到1,表示機率。綠色的O表示容許的機率nu。紅色的X表示不容許的機率nu。我們將紅色彈珠視為一筆錯誤的資料,那麼母體有40%的資料是錯誤的,所以若樣本裡面,若有0.4機率的資料是錯誤的,那麼這個樣本就可以代表母體。但實際情況是,樣本裡發生錯誤資料的機率,不見得剛好是0.4,所以我們就定一個範圍epsilon = 0.3為我們容許的誤差範圍。
接下來,我們想算出,在樣本數量為10的情況下,出現紅色球 (錯誤資料)的機率P。有兩種方法:
方法一:用Hoeffding's Inequality
此法不需要知道,紅色彈珠在母體的機率mu,與紅色彈珠在樣本的機率nu。只要知道樣本的數量N與容忍度epsilon,就可以馬上算出P。
方法二:將上圖的紅叉標示的機率加總:
P = P[#=0] + P[#=8] + P[#=9] + P[#=10] = 0.0183
我將方法二的計算過程,寫在MAC的Numbers App或Windows的Excel,並顯示結果。
我用MAC的Numbers App 做成下面這張表:
- Marble: 罐子裡彈珠數,不知道。
- R (Red): 罐子裡紅色彈珠數,不知道。紅色彈珠可視為一筆錯誤的資料。
- G (Green): 罐子裡綠色彈珠數,不知道。綠色彈珠可視為一筆正確的資料。
- mu = 紅色彈珠佔罐子裡彈珠40%。
- Samples = 樣本數量。
- epsilon = 容忍度。若將紅色彈珠視為錯誤資料,那麼|母體有錯誤資料的機率 - 樣本有錯誤資料的機率|<= epsilon為我們容許,epsilon為容許的誤差上限,簡稱容忍度。
第二張表:
- R = 樣本裡紅色彈珠的數量。
- G = 樣本裡綠色彈珠的數量。
- N = 在樣本裡,紅色彈珠的數量為R,綠色彈珠的數量為G的情況下,有機種排列方式
- P(D) = 在某一組樣本D裡,出現紅色彈珠的數量為R,綠色彈珠的數量為G,的機率
- nu = 紅色彈珠出現在樣本的機率。
- |nu - mu| = |母體有錯誤資料的機率 - 樣本有錯誤資料的機率|
- Is Bad? = V。表示:誤差 |nu = mu| > 容忍度 epsilon。
從彈珠罐取放彈珠10次(Sampling with Replacement),10次裡面出現紅色綠色彈珠,有11種情況,分別是D1, D2, …, D11。於是我們用高中學過的排列組合,將這個問題,拆成11個獨立的小問題:
- D1:出現10個紅色的,及0個綠色的,
- D2:出現9個紅色的,及1個綠色的。
- D3:出現8個紅色的,及2個綠色的。
- D4:出現7個紅色的,及3個綠色的。
- D5:出現6個紅色的,及4個綠色的。
- D6:出現5個紅色的,及5個綠色的。
- D7:出現4個紅色的,及6個綠色的。
- D8:出現3個紅色的,及7個綠色的。
- D9:出現2個紅色的,及8個綠色的。
- D10:出現1個紅色的,及9個綠色的。
- D11:出現0個紅色的,及10個綠色的。
有了所有小問題的R和G之後,我們就可以計算每個小問題發生的機率。例如,求D3發生的機率的公式為:
其它小問題的機率。我將此公式,套用在Numbers,就可以很快算出來,如:
N:D2
FACT是Numbers提供的公式。如 FACT (3) = 3! = 6
P(D):D2
我們發現,把所有小問題的機率加起來,剛好為100% = P(D):Sum格子。更加驗證了,這個大問題,剛好拆解成11個小問題,而且不會漏掉。
用方法一和方法二,所算出來的P,分別為0.33與0.0183,這有些差異。問題出在那兒?問題出在樣本數量不夠大。如果樣本數量愈大,這個差異就愈小。如何說明?
先不用數學證明這個現象。取而代之,我寫了一支Python程式,解釋這個現象。Python程式,計算出下面的結果:
在樣本為10的情況下,此Python的結果,和用Mac Numers的結果是一樣的。
此程式接下來也畫了下面這張圖,樣本數N從10逐一增加到30,用方法一和方法二所計算的P,隨者N愈大,這兩個P就愈小,而且愈接近。
總結上圖所發現的幾件事情:
- 當樣本數量夠大,方法二算出來的P,會接近方法一,由Hoeffding's Inequality算出來的P。所以Hoeffding's Inequality是此問題的上限。
- 不管是用方法一,還是方法二,樣本數量都要夠大,這樣我們不希望看到的機率P,就會愈小。
Python程式如下:
[InferHoeffding.py]
-Count